skip all navigation
skip banner links
skip primary navigation

A Geologic Odyssey: Models and Results

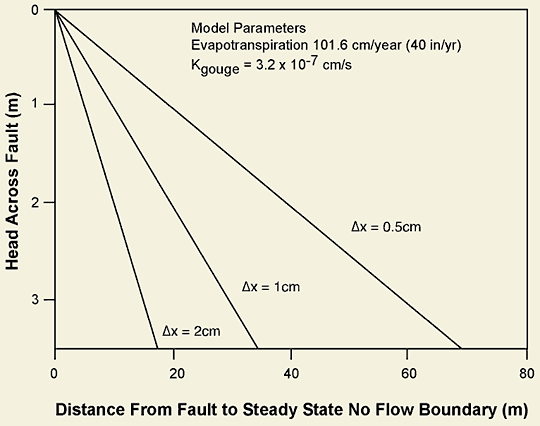
The distance from the fault to a steady-state no-flow boundary depends on the head, evapotranspiration rate (assumed to be 101.6 cm/yr [40 in/yr]), and the thickness of the fault gouge (KGouge = 3.2x10 -7 cm/s).

We developed a simple steady-state model to determine the distance that water can move into the unsaturated zone before evapotranspiration depletes it. In the initial model, homogeneous plug flow is assumed (rather than fingered flow through "holes" in the fault gouge, which would be more realistic, but more difficult to model). Initial transient flow immediately after faulting is ignored. Porosity is assumed to be 30 percent. Fault gouge thickness was modeled at 2, 1, and 0.5 cm.

The steady-state model takes n cells 1 cm thick, 1 cm wide and 100 cm long. Water (Qin) moves into end of a cell, evapotranspiration is subtracted from the top of the cell (rate of 6.44 x 10-6 cm/sec times 100 cm length) and water (Qout) is passed to the adjacent cell until a steady-state no-flow boundary is reached. The equations used in the model are:

Qout = Qin - E

where

  • Qin = flow into cell (cm3/cm2 x s)
  • E = evapotranspiration (40 in/yr = 101.6 cm/yr; 101.6 cm/365x60x60x24 = 3.22 x 10-6 cm/sec)
  • Qout = K x dh/dl x A x 100 - (100 cm x 6.44 x 10-6 cm/sec)

To calculate Qout for cells 2 to N

  • Qout = Cell i-1 - (100 x 3.22 x 10-6) until a steady-state no-flow boundary is reached
  • K = gouge permeability in cm/s (assumed 3.2 x 10-7 cm/sec)
  • dh = head in cm
  • dl = gouge thickness
  • A = cross sectional area in cm2
Volume (liters) passing through 1cm2 gouge in 10 years.
Volume (liters) passing through 1cm2 gouge. The volume of water passing through fault gouge depends on the head and the thickness of the fault gouge (KGouge = 3.2-7cm/s)

We also constructed a model to estimate how long the cementation process could continue before all of the available porosity was plugged. This model simply calculates, based on water saturated with calcium carbonate and a 30% porosity, how long it will take to pass enough water through the gouge that contains enough calcium carbonate to completely fill the pores in the predicted cementation zone.

Model of time required to fill 30 percent porosity with calcium carbonate by evapotranspiration alone.

  • Tvp = total volume to plug 1 cm2 corridor (1 cm2 x distance x 0.3)
  • Tvf = total volume of fluid to plug 1 cm2 corridor with calcite (1 cm2 x distance x 0.3) = Tvp/(saturation of calcite in water/density of calcite) (0.000014g/l/2.93g/cm3)
  • Time = Tvf/Q (total volume of fluid divided by discharge)
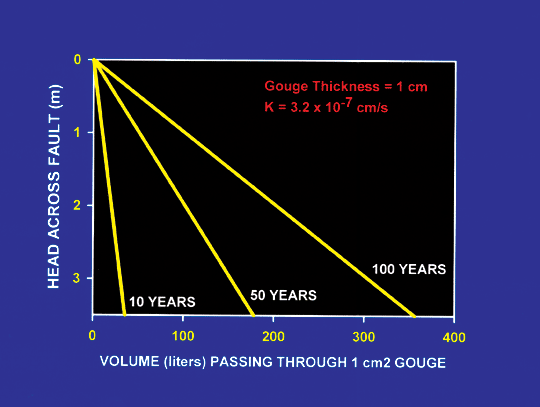
  • Q = K x dh/dl x A
  • A = 1 (cm2)
  • dh = head in cm
  • dl = gouge thickness (cm)
  • K = gouge permeability in cm/s (assumed 3.2 x 10-7 cm/sec)

The distance that cementation extends from the fault increases linearly from zero at the water table on the up-thrown block to about 34 m at a head of 3.5 m for a fault gouge thickness of 1.0 cm. The distance is less than 19 m for a 2-cm-thick gouge.