New Mexico Geochronology Research Laboratory
K/Ar and ⁴⁰Ar/³⁹Ar Methods

Overview

Isotopes of Potassium and Argon

The isotopes the KAr system relies on are Potassium (K) and Argon (Ar). Potassium, an alkali metal, the Earth's eighth most abundant element is common in many rocks and rock-forming minerals. The quantity of potassium in a rock or mineral is variable proportional to the amount of silica present. Therefore, mafic rocks and minerals often contain less potassium than an equal amount of silicic rock or mineral. Potassium can be mobilized into or out of a rock or mineral through alteration processes. Due to the relatively heavy atomic weight of potassium, insignificant fractionation of the different potassium isotopes occurs. However, the ⁴⁰K isotope is radioactive and therefore will be reduced in quantity over time. But, for the purposes of the KAr dating system, the relative abundance of ⁴⁰K is so small and its half-life is so long that its ratios with the other Potassium isotopes are considered constant.

Argon, a noble gas, constitutes approximately 0.1-5% of the Earth's present day atmosphere. Because it is present within the atmosphere, every rock and mineral will have some quantity of Argon. Argon can mobilized into or out of a rock or mineral through alteration and thermal processes. Like Potassium, Argon cannot be significantly fractionated in nature. However, ⁴⁰Ar is the decay product of ⁴⁰K and therefore will increase in quantity over time. The quantity of ⁴⁰Ar produced in a rock or mineral over time can be determined by substracting the amount known to be contained in the atmosphere. This is done using the constant ⁴⁰Ar/³⁶Ar ratio of atmospheric Argon. This ratio is 295.5.

Radioactive decay of parent isotope to daughter isotope

The nuclei of naturally occurring ⁴⁰K is unstable, decaying at a constant rate (half-life = 1.25 billion years). The decay scheme is electron capture and positron decay. About 89% of the ⁴⁰K atoms will decay to ⁴⁰Ca. For the K/Ar dating system, this decay scheme to calcium isotopes is ignored. The remaining 11% of the ⁴⁰K atoms decay to ⁴⁰Ar. It is this scheme that makes the K/Ar method work.

The buildup of radiogenic ⁴⁰Ar (⁴⁰Ar*) in a closed system can be expressed by the equation:

 

The K/Ar Dating technique

General assumptions for the Potassium-Argon dating system

Certain assumptions must be satisfied before the age of a rock or mineral can be calculated with the Potassium-Argon dating technique. These are:

• The material in question is a closed system. In other words, no radiogenic ⁴⁰Ar has escaped from the rock/mineral since it formed. In the case of a volcanic mineral, this means rapid cooling. Likewise, potassium has not been gained or lost.
• A correction is made for atmospheric argon (⁴⁰Ar from the ⁴⁰Ar/³⁶Ar ratio = 295.5 subtracted).
• No non-atmospheric ⁴⁰Ar was incorporated into the rock/mineral during or after its formation.
  
• The isotopes of potassium in the rock/mineral have not fractionated, except by ⁴⁰K decay.
  
• The decay constants of ⁴⁰K are accurately known.
  
• The quantities of ⁴⁰Ar and potassium in the rock/mineral are accurately determined.

The K/Ar age determination

Once the ⁴⁰Ar and potassium in a rock/mineral are accurately measured, the amount of ⁴⁰K (based on the relative abundance of ⁴⁰K to total potassium) and ⁴⁰Ar* (radiogenic ⁴⁰Ar) must be calculated. The K/Ar method uses a spike (known quantity) of ³⁸Ar mixed with the argon extracted from the rock/mineral to determine the quantity of ⁴⁰Ar*. The resulting ⁴⁰Ar* and 40K can be plugged into the age equation as follows:

 

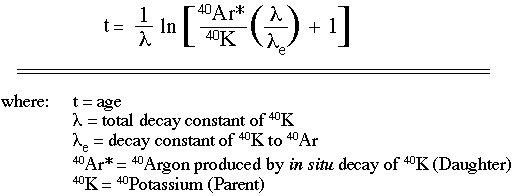
Problems and Limitations of the K/Ar dating technique

Because the K/Ar dating technique relies on the determining the absolute abundances of both ⁴⁰Ar and potassium, there is not a reliable way to determine if the assumptions are valid. Argon loss and excess argon are two common problems that may cause erroneous ages to be determined. Argon loss occurs when radiogenic ⁴⁰Ar (⁴⁰Ar*) produced within a rock/mineral escapes sometime after its formation. Alteration and high temperature can damage a rock/mineral lattice sufficiently to allow ⁴⁰Ar* to be released. This can cause the calculated K/Ar age to be younger than the "true" age of the dated material. Conversely, excess argon (⁴⁰Ar_E) can cause the calculated K/Ar age to be older than the "true" age of the dated material. Excess argon is simply ⁴⁰Ar that is attributed to radiogenic ⁴⁰Ar and/or atmospheric ⁴⁰Ar. Excess argon may be derived from the mantle, as bubbles trapped in a melt, in the case of a magma. Or it could be a xenocryst/xenolith trapped in a magma/lava during emplacement.

The ⁴⁰Ar/³⁹Ar Dating technique

Principles of the ⁴⁰Ar/³⁹Ar method

The ⁴⁰Ar/³⁹Ar dating technique is a more sophisticated variation of the K/Ar dating technique. Both techniques rely on the measurement of a daughter isotope (⁴⁰Ar) and a parent isotope. While the K/Ar technique measures potassium as the parent, the ⁴⁰Ar/³⁹Ar technique uses ³⁹Ar.

Because the relative abundances of the potassium isotopes are known, the ³⁹Ar_K (produced from ³⁹K by a fast neutron reaction) can be used as a proxy for potassium. Therefore, unlike the conventional K/Ar technique, absolute abundances need not be measured. Instead, the ratios of the different argon isotopes are measured, yielding more precise and accurate results. Additional advantages of the single isotopic measurements of the ⁴⁰Ar/³⁹Ar technique are decreased effects of sample inhomogeneity and the use of smaller sample sizes.

Sample Irradiation / Production of ³⁹Ar

Because ³⁹Ar_K can only be produced by a fast neutron reaction on ³⁹K [ ³⁹K(n,p)³⁹Ar ], all samples dated by the ⁴⁰Ar/³⁹Ar technique must be irradiated in the core of a nuclear reactor. The amount of ³⁹Ar_K produced in any given irradiation will be dependant on the amount of ³⁹K present initially, the length of the irradiation, the neutron flux density and the neutron capture cross section for ³⁹K. However, because each of these parameters is difficult to determine independantly, a mineral standard, or monitor, of known age is irradiated with the samples of unknown age. The monitor flux can then be extrapolated to the samples, thereby determining their flux. This flux is known as the 'J' and can be determined by the following equation:

 

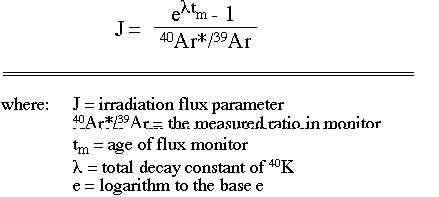
In addition to ³⁹Ar production from ³⁹K, several other 'interference' reactions occur during irradiation of the samples. Other isotopes of argon are produced from potassium, calcium, argon and chlorine. These are:

 

As the table above illustrates, several "undesirable" reactions occur on isotopes present within every geologic sample. These reactor produced isotopes of argon must be corrected for in order to determine an accurate age. The monitoring of the interfering reactions is performed through the use of laboratory salts and glasses. For example, to determine the amount of reactor produced ⁴⁰Ar from ⁴⁰K, potassium-rich glass is irradiated with the samples. The ⁴⁰Ar/³⁹Ar ratio of the glass is then measured in the mass spectrometer to determine the correction factor that must be applied to the rest of the samples in that irradiation. CaF is also routinely irradiated and measured to determine the ³⁶Ar/³⁷Ar and ³⁹Ar/³⁷Ar correction factors. The "desirable" production of ³⁷Ar from ⁴⁰Ca allows us determine how much ³⁶Ar and ³⁹Ar to correct for, as well as the K/Ca ratio of the sample. The desirable production of ³⁸Ar from 37Cl allows us to determine how much chlorine is present in our samples. A salt of KCl is irradiated to determine the ³⁸Ar/³⁹Ar production ratio which can then be applied to other samples to determine K/Cl ratios.

⁴⁰Ar/³⁹Ar age determination

Once the J (neutron flux parameter), ⁴⁰Ar* and ³⁹Ar_K have been determined (ie. subtracting atmospheric argon, system blank and interferring reactor produced isotopes), they can be included in the ⁴⁰Ar/³⁹Ar age equation:

 

Because the ⁴⁰Ar/³⁹Ar technique relies on ratios instead of absolute quantities, we are able to extract and measure multiple aliquots of argon from a single sample. Multiple argon extractions can be performed on a sample in several ways. Step-heating is the most common way and involves either a furnace or a laser to uniformily heat the sample to evolve argon. The individual ages from each heating step are then graphically plotted on an age spectrum or an isochron. Mechanical crushing is also a technique capable of releasing argon from a single sample in multiple steps.

Laser probes also allow multiple ages to be determined on a single sample aliquot, but do so using accurate and precise spatial control. For example, laser spot sizes of 100 microns or less allow a user to extract multiple argon samples from across a small mica or feldspar grain. The results from a laser probe can be plotted in several graphical ways, including a map of a grain showing lateral argon distribution.

⁴⁰Ar/³⁹Ar total fusion of a sample is comparable to a K/Ar age determination in that it relies on wholesale release of argon at one time. However, unlike conventional K/Ar, ⁴⁰Ar/³⁹Ar total fusion measures ratios, making it ideal for samples known to be very argon retentive (eg. sanidine). Total fusion is performed using a laser and results are commonly plotted on probability distribution diagrams or ideograms.

Some problems with the ⁴⁰Ar/³⁹Ar technique.

Standard Intercalibration

In order for an age to be calculated by the ⁴⁰Ar/³⁹Ar technique, the J parameter must be known. For the J to be determined, a standard of known age must be irradiated with the samples of unknown age. Because this (primary) standard ultimately cannot be determined by ⁴⁰Ar/³⁹Ar, it must be first determined by another isotopic dating method. The method most commonly used to date the primary standard is the conventional K/Ar technique. The primary standard must be a mineral that is homogeneous, abundant and easily dated by the K/Ar and ⁴⁰Ar/³⁹Ar methods. Traditionally, this primary standard has been a hornblende from the McClure Mountains, Colorado (a.k.a. MMhb-1). Once an accurate and precise age is determined for the primary standard, other minerals can be dated relative to it by the ⁴⁰Ar/³⁹Ar method. These secondary minerals are often more convenient to date by the ⁴⁰Ar/³⁹Ar technique (e.g. sanidine). However, while it is often easy to determine the age of the primary standard by the K/Ar method, it is difficult for different dating laboratories to agree on the final age. Likewise, because of heterogeneity problems with the MMhb-1 sample, the K/Ar ages are not always reproducible. This imprecision (and inaccuracy) is transferred to the secondary minerals used daily by the ⁴⁰Ar/³⁹Ar technique. Fortunately, other techniques are available to re-evaluate and test the absolute ages of the standards used by the ⁴⁰Ar/³⁹Ar technique. Some of these include other isotopic dating techniques (e.g. U/Pb) and the astronomical polarity time scale (APTS).

Decay Constants

Another issue affecting the ultimate precision and accuracy of the ⁴⁰Ar/³⁹Ar technique is the uncertainty in the decay constants for ⁴⁰K. This uncertainty results from 1) the branched decay scheme of ⁴⁰K and 2) the long half-life of ⁴⁰K (1.25 billion years). As technology advances, it is likely that the decay constants used in the ⁴⁰Ar/³⁹Ar age equation will become continually more refined allowing much more accurate and precise ages to be determined.

J Factor

Because the J value is extrapolated from a standard to an unknown, the accuracy and precision on that J value is critical. J value uncertainty can be minimized by constraining the geometry of the standard relative to the unknown, both vertically and horizontally. The NMGRL does this by irradiating samples in machined aluminum disks where standards and unknowns alternate every other position. J error can also be reduced by analyzing more flux monitor aliquots per standard location.

³⁹Ar Recoil

The affects of irradiation on potassium-bearing rocks/minerals can sometimes result in anomalously old apparent ages. This is caused by the net loss of ³⁹Ar_K from the sample by recoil (the kinetic energy imparted on a ³⁹Ar_K atom by the emission of a proton during the (n,p) reaction). Recoil is likely in every potassium-bearing sample, but only becomes a significant problem with very fine grained minerals (e.g. clays) and glass. For multi-phase samples such as basaltic wholerocks, ³⁹Ar_K redistribution may be more of a problem than net ³⁹Ar_K loss. In this case, ³⁹Ar may recoil out of a low-temperature, high-potassium mineral (e.g. K-feldspar) into a high-temperature, low potassium mineral (e.g. pyroxene). Such a phenomenon would great affect the shape of the age spectrum.

References

1. McDougall, I., and Harrison, T.M., 1999, Geochronology and thermochronology by the ⁴⁰Ar/³⁹Ar method: New York, Oxford University Press, xii, 269 p.